Overview
The /jobgraph folder contains tools for writing thread-parallel code based upon MyraMath's JobGraph concept. A JobGraph is a container of executable code statements, along with their captured referential environment, much like a closure or a C++11 lambda function. However, in contrast to a C++11 lambda, a JobGraph executes in parallel over multiple threads, not serially.
All of MyraMath's parallel algorithms (like the BLAS3/LAPACK routines in /pdense and the Solver's in /multifrontal) are implemented in terms of JobGraph's. Users can compose their own higher-level JobGraph's by combining the low-level ones already defined in Myramath (see ParallelJobGraph, SequentialJobGraph and FusedJobGraph). Alternatively, users can create their own low-level JobGraph's from the bottom-up using UserJobGraph and LambdaJobGraph. Tools for debugging and visualizing JobGraph's are also available.
Below are links to the sections of this page:
- What is a JobGraph?
- Executing existing JobGraph's
- Composing JobGraph's
- User-defined JobGraph's
- Debugging Tools
What is a JobGraph?
The JobGraph class (and the /jobgraph ecosystem) is a small toolkit for building thread-parallel C++ programs. Like OpenMP, JobGraph is a shared-memory programming model designed for multicore machines. OpenMP is typically used to parallelize embarrassingly parallel for-loops of homogeneous code using "bolted-on" #pragma's (a SIMD-like model). In contrast, JobGraph is task-based, where heterogeneous fragments of code (Job's) are processed asynchronously according to their declared dependencies (a MIMD-like model). JobGraph is more intrusive, but can be applied to a wider variety of workloads and "scales up" more naturally using a language of composition.
Consider the example psuedocode below, which performs A=L*L' (Cholesky) decomposition of a 4x4 block matrix:
In its current form, this code is rather resistant to bolt-on parallelization using #pragma omp parallel for directives. Each iteration of the outermost loop (k) carries many dependencies from the previous iteration, disqualifying it from parallelization. And the body of the k-loop has a heterogeneous payload of various sub-loops, but no single for-loop has an especially large iteration count. Assuming all tasks take equal time, adding pragma's to the two embarrassingly parallel loops (the trsm() loop and the gemm() loop) will yield the following speedup:
The total time to complete the algorithm was reduced from 20 units (left column) to 16 units (middle column), not great but perhaps commensurate with the level of programming effort. A particularly painful artifact of the current implementation is that the potrf(1) task, which only depends upon three other tasks (potrf(0), trsm(0,1), and syrk(0,1)), is only performed at time t=8 even with OpenMP parallelization. Delays like this lead to a needlessly long "tail" of computation. It would be preferable to start that task much sooner, but the code (in its current form) does a poor job of expressing the minimal critical path of dependencies to execute potrf(1).
This discussion is admittedly unfair to OpenMP, as there are smarter ways to parallelize this algorithm by reorganizing it and using more advanced OpenMP directives (the tasking model). JobGraph is exactly that sort of reorganization. A careful tabulation of all the read/write dependencies of the algorithm into a directed acyclic graph yields the following result:

Click here to view fullsize image.
If every Job was executed as soon as its critical path allowed it, considerable time savings could be accumulated (right column). Since potrf(0) has no prior dependencies, execution would begin() there immediately at t=1. All of the trsm(0,*) Job's can then run at t=2, just like the #pragma case. However, the JobGraph approach pulls ahead at t=3, as all of the syrk(0,*) and gemm(0,*,*) Job's can be executed in parallel (despite their heterogeneity), a concept that is difficult to express using bolt-on #pragma's. This results in higher resource utilization (up to six active processing units instead of three) and enables potrf(1) to execute as early as t=4. Further gains accumulate for k=1 and k=2. As the potrf(3) has no subsequent dependencies, execution will end() there at t=10, in roughly half the time as the original serial algorithm.
Executing existing JobGraph's
All of MyraMath's parallel algorithms are implemented in terms of JobGraph. For example, pdense/pgemm.h defines an "immediate" routine, pgemm_inplace(), that calculates C := alpha*A*B + beta*C in parallel, but it also defines a "deferred" version, pgemm_jobgraph(). Calling pgemm_jobgraph() requires the same arguments as pgemm_inplace(), but it doesn't actually calculate anything. Instead, it captures the arguments to the function (like a C++11 lambda) and returns a JobGraph that can "fulfill" the calculation at some point in the future, when you call execute() upon it.
All of the algorithms in /pdense follow the same pattern: exposing an "immediate" version and a "deferred" version that does nothing but return a JobGraph, denoted with a _jobgraph() suffix in the function name. The following _jobgraph() routines are exposed:
-
pgemm_jobgraph(), performs general matrix-matrix multiplication -
ptrmm_jobgraph(), multiplies by a triangular matrix -
ptrsm_jobgraph(), backsolves by a triangular matrix -
psyrk_jobgraph(), performs a symmetric rank-k update -
psyr2k_jobgraph(), performs a symmetric rank-2k update -
pherk_jobgraph(), performs a hermitian rank-k update -
pher2k_jobgraph(), performs a hermitian rank-2k update -
phemm_jobgraph(), multiplies by a hermitian matrix -
psymm_jobgraph(), multiplies by a symmetric matrix -
ppotrf_jobgraph(), performs L*L' decomposition of a symmetric positive matrix -
psytrf_jobgraph(), performs L*D*L' decomposition of a symmetric matrix -
phetrf_jobgraph(), performs L*D*L' decomposition of a hermitian matrix -
pgetrf_jobgraph(), performs L*U decompositions of a general matrix
The parallel algorithms in /multifrontal are typically member functions of a Solver class, not free-standing non-member functions. Each Solver offers both an "immediate" version and "deferred" _jobgraph() version of the following algorithms:
-
Solver.factor_jobgraph(), decomposes a sparse A into triangular factors -
Solver.solve_jobgraph(), performs sparse backsolution -
Solver.schur_jobgraph(), forms a sparse B'*inv(A)*B schur complement -
Solver.inverse_jobgraph(), samples inverse(A) -
Solver.partialsolve_jobgraph(), performs sparse backsolution
Consult the source level documentation for each of these algorithms for further details.
Composing JobGraph's
On their own, the _jobgraph() versions of all these algorithms might seem superfluous. In particular, why bother capturing the JobGraph of an algorithm only to execute() it later, when you could just call the "immediate" version at that time instead? The answer is that these atomic JobGraph's can be composed together into larger ones, in such a way that they expose more opportunities for parallelism and therefore run faster.
The main tool for this kind of composition is ParallelJobGraph (and the parallelize() helper function). It's deceptively simple: given a collection of independent JobGraph's (in the sense that they do not have any read/write hazards among their captured arguments, embarrassingly parallel), ParallelJobGraph combines them into a larger one. Consider tutorial/jobgraph/ParallelJobGraph.cpp, listed below, which computes the Cholesky decomposition of two Matrix's (A1 and A2) at the same time:
Composing JobGraph's like this can yield meaningful speedups (say 10-20%) with little programming effort required. The figure below depicts the resulting ParallelJobGraph and helps explain why it can be faster: by aggregating the two ppotrf_jobgraph() calls into one, multiple processing units (at least two) can consistently be put to use, even as each individual factorization draws to a close.

Click here to view fullsize image.
The complementary class to ParallelJobGraph is SequentialJobGraph (and the sequentialize() helper function). This class is used to compose two (or more) JobGraph's that (unfortunately) have some sort of data hazard. Perhaps the outputs of one JobGraph are the inputs to the next? Or multiple JobGraph's would "race" to update the same output quantity? Both of these cases would require the use of a SequentialJobGraph to enforce the dependency. Consider tutorial/jobgraph/SequentialJobGraph.cpp, which builds on the previous example:
Instead of just factoring A1 and A2, this example parallelizes a pair of "factor/solve/check" problems. The two problems are independent, but the various substages require sequence points (you must factor A1 before you can solve X1=A1\B1, and you must solve for X1 before you can form the residual R1=A1*X1-B1). SequentialJobGraph and/or sequentialize() can be used to enforce these sequence points, but still returns JobGraph's suitable for parallelize()'ing later. Conceptually, sequentialize()'ing two JobGraph's g1 and g2 is straightforward: just add a dependency (an edge) from every end() Job of g1 into every begin() Job of g2. The figure below depicts the final JobGraph:

Click here to view fullsize image.
The last compositional tool to discuss is FusedJobGraph. The tools introduced so far have been "black-or-white" in their approach to describing dependencies between subgraphs. At one extreme, ParallelJobGraph is used to indicate two JobGraph's g1 and g2 are embarassingly parallel (none of the Job's in g2 depend upon any Job in g1). On the other hand, SequentialJobGraph is used to indicate total dependency (none of the Job's in g2 can begin until every Job in g1 is finished). To cover the "gray" area between these two extremes, there is FusedJobGraph.
To motivate FusedJobGraph, consider the psuedocode snippets below. They encode the four substages to solving A*X=B for symmetric positive A: (i) Cholesky factorization for A=L*L', (ii) forward solution to find X=L\B, (iii) back solution to find X=L'\B, and (iv) multiplication to form the residual R=B-A*X.
In the previous section, it was pointed out that the substages (i) through (iv) are not embarrassingly parallel, so a SequentialJobGraph was used to sequence them. However, a closer inspection reveals that assuming this kind of "total dependency" is a pessimization. For example, the first "row" of the forward solution stage, X(0,:)=L(0,0)\B(0,:), could be started as soon as the first pivot factorization A(0,0)=L(0,0)*L(0,0)' is complete. The code listing below, tutorial/jobgraph/FusedJobGraph.cpp carefully encodes the minimum set of fine-grained dependencies between (i)-(iv) into a FusedJobGraph.
The resulting FusedJobGraph is shown below (left). The various substages are color-coded for ease of reading. For sake of comparison, a SequentialJobGraph that performs the exact same work is shown below, too (right). As demonstrated by the output of the test program above, the FusedJobGraph runs about 20-30% faster than the SequentialJobGraph, because removing these "total dependency" pessimizations shrinks the critical path of execution considerably.

Click here to view fullsize image.
For better or worse, FusedJobGraph is a specialist's tool. Like the other compositional JobGraph's, FusedJobGraph is nothing more than a container for other subgraphs. However, the user is required to correctly encode all of the fine-grained inter-subgraph dependencies explicitly, a task that demands fairly deep knowledge of the underlying algorithms and how they are mapped onto JobGraph's. That said, MyraMath does use this technique internally (/multifrontal algorithms are basically fused collections of /pdense algorithms), so it is exposed for the advanced user.
User-defined JobGraph's
To complement the top-down compositional tools described above, there is also a UserJobGraph, useful for constructing arbitrary JobGraph's from the bottom-up. Arbitrary code (Job's) in the form of C++11 lambda's can be injected using UserJobGraph.insert(), then UserJobGraph.add_edge() is used to specify dependencies. Once finished, the graph can either be execute()'d, or further composed using parallelize() or sequentialize(), just like any other JobGraph. The code example below, tutorial/jobgraph/UserJobGraph.cpp shows the idea in action, implementing a single level of the Strassen algorithm to parallelize Matrix*Matrix multiplication:
The JobGraph produced by this example is shown below:
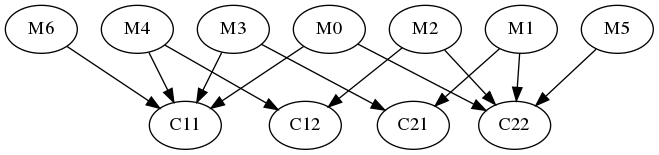
LambdaJobGraph (and the make_LambdaJobGraph() helper function) are close relatives of UserJobGraph. They provide syntactic sugar for a UserJobGraph that contains exactly one Job (again, in the form of a C++11 lambda). The code example below, tutorial/jobgraph/LambdaJobGraph.cpp, shows them in action, by stringing together a few messages:
The JobGraph produced by this example is shown below:
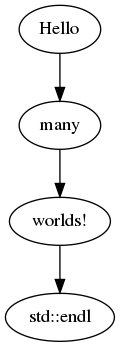
Debugging Tools
Debugging parallel algorithms can be problematic, mainly because their non-deterministic order of execution impedes reproducibility. JobGraph can be unforgiving in this regard, but there are a few tools available to aid debugging. The first is verify(const JobGraph& g), which can probe a JobGraph g for some common bugs (the presence of a cycle of dependencies, check reflexivity of parent/child relationships between Job's, etc). If verify(g) reports any problems, it's likely that execute(g) will deadlock, crash or otherwise misbehave. Unfortunately the converse isn't necessarily true. That is, even if verify(g) reports no problems, that's not sufficient to guarantee correctness/termination of execute(g), because g could have failed to encode/report every dependency between Job's. Put another way, execute() might reveal new bugs that verify() cannot detect.
The next debugging tool that's worth mentioning is graphviz(const JobGraph& g). It traverses all the Job's in g, and encodes the dependencies among them as a DAG in .dot format. This the native input format for Graphviz, a powerful graph drawing tool that can typeset/visualize the JobGraph into a variety of output formats (.pdf, .png, many more). All the JobGraph figures on this page were generated using graphviz(g). In practice, graphviz(g) is particularly useful when one is trying to reason about g in order to incorporate it into a higher-level FusedJobGraph.
When verify(g) reports no problems, and graphviz(g) looks as expected, but execute(g) misbehaves in some way (for instance, it terminates but computes the wrong answer), it might be worth trying execute_serial(g). This has the exact same signature/semantics as execute(g), but always uses a single thread. It is particularly useful for detecting "write" races, where two Job's modify the same output but there is no dependency/sequence enforced between them. Under such circumstances, execute_serial(g) will give the right answer (because it will tacitly eliminate the race) but execute(g) will not.
A final piece of advice: when developing new JobGraph's, try to separate their topological aspects from their computational aspects as much as possible. For instance, bake the topological aspects (parent/child relationships) into a base class that implements only dummy printf()'s for the computational payload, then implement the real computational routines via overrides within a derived class, later. This allows the topological part (the dependencies) to be tested independently and quickly using verify(g), graphviz(g). You can even execute(g) or execute_serial(g) with the payload of printf() statements, to examine a few permissible sequences of execution. All of the existing JobGraph's maintain this topological/computational separation.
Go back to API Tutorials
 1.8.13
1.8.13